I’m Justin Bao, and over the past few years I have been on a personal journey into the world of mathematics. The subject has fascinated me and I have engaged myself in the community through competitions, presentations, and being involved in Maths Club. In particular, my focus has been on providing myself a rigorous understanding and foundation of mathematics as a whole.

Therefore, I would like to present one of the earlier proofs I did on a fact that seems fairly intuitive, that, if the square root of a number is an integer, it implies the number is a perfect square.

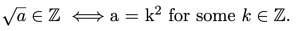
This is an idea which, I believe, many people have used, without having it properly and rigorously proven to them. Why is mathematical rigour important? Whether we’re mathematicians, engineers, physicists, or statisticians, we must be 100% confident that the equations we use are infallible, that there are no thresholds or cases where the theorem fails. Therefore, even as obvious facts as this one must be rigorously proven.

When tackling the proof of such an intuitive theorem, I have found it most important to tking about ways the theorem might be disproven. For this question, it might intuitively look like there exists some threshold for large numbers that allows them to not need to be a perfect square to have an integer square root. This is why, so often, the simplest theorems in mathematics have difficult proofs because of how hard it is to visualize ways the theorem can fail. For this theorem, I used a fairly common proof technique which is proof by contradiction, where we assume the theorem to be false, exhibit a contradiction, and conclude that our initial assumption was false. Such a proof is nonconstructive (it tells us merely that a perfect square exists, but doesn’t tell us what it is), and requires the acceptance of the Axiom of Choice.

I encourage you to investigate a constructive proof of the theorem (one that lets us pinpoint exactly what the perfect square is), and determine for yourself whether you accept this. Furthermore, a direct implication of this problem is that the square root of all non-square numbers is irrational. Throughout the proof, I implore you to pay particular attention to the steps I took to truncate the problem in order to make it simpler, and see how that idea is applied in many areas of mathematics and STEM in general.

I hope you enjoy the proof, and that, after, you will build a greater appreciation for this comparably more boring aspect of mathematics. Please feel free to reach out to me if you have any questions and you can access the proof below.